Sıfır Hipotezası və T testi
Bir öncəki yazıda bəhs etdiyimiz Reqressiya analizi haqqında ümumi məlumatları başa düşmək çox vacib məsələdir. Reqressiya analizi bir bina tikintisi kimidir və binanın əsasını qoymadan ümumən bina haqqında danışmaq mənasızdır. Binanın necə tikilməyi isə data analizinin məqsədindən və analizin aparıldığı sahədən asılıdır.
Binanın necə tikilməyi barədə danışsaq gərək biz risk menecmenti, marketinq və s. sahələrin hər birini ayrı-ayrı araşdıraq və hər şərt üçün müxtəlif dəyişənləri analiz edək. Amma onların arasında necə əlaqənin olmağı isə, necə deyərlər, “beynəlxalq standart”dır. Təbii ki, mən burda əlaqə deyəndə birinci yazıda haqqında bəhs etdiyim ilkin anlayışlardan bəhs etmirəm. İkinci yazımızda biz daha dolğun, daha professional amillərdən bəhs edəciyik.
Bəli, reqressiya analizinin ən mühüm sahələrindən biri də aldığımız model üzərində müxtəlif testlər edə bilməkdir. Daha ali səviyyədə data analitikası daxilində onlarla teslər mövcuddur. Demək olar ki, bütün testləri edərkən bizə lazım olan məfhum isə Null Hypothesis, yəni Sıfır hipotezi nəzərdə tutulur. Şərti qaydada biz sıfır hipotezini H₀ ilə işarə edirik. Buna alternativ olaraq bizdə H₁ hipotezi də vardır ki, bu da əsasən birinci hipotezanı inkar edir.
Testləri öyrənərkən sizin iki variantınız vardır: ya testi tam dərk edib analizi başa düşərək aparmaq, ya da məğzi dərk etmədən testi aparmaq. İki variantda da biz testi edə bilər, cavabı ala bilərik. Amma məsələ aldığımız nəticəni nəyəsə tətbiq etməyə gələndə ikinci yolla edənlərin problemləri üzə çıxa bilir və bu qaçılmaz faktdır. Təcrübə də onu göstərir ki, reqressiya testlərinin mahiyyətinin dərk edilməməsinin ən böyük səbəbi bizə verilən hipotezi başa düşməməyimizdir. İlk olaraq sıfır hipotezini aydın şəkildə başa düşmək lazımdır, onu başa düşdükdən sonra biz özümüzdə “Mən bu testi niyə edirəm?” sualına cavab verə bilərik. Əgər bu məsələ həll edilibsə, geridə qalan hissə, testi etmək və nəticəni nəyəsə tətbiq etmək hissəsi çox rahatdır. Ən əfsus, yazı boyunca mən Eviews statistik proqramından istifadə edəcəm ki, testin pərdəarxası hissəsi ilə vaxtımızı boşuna sərf etməyək.
Sıfır hipotezini və test üçün lazım olan digər mühim faktorları mən t-test üzərində izah edəcəm, çünki o, ən asan mövzu hesab olunur və qaydaları onun üzərində tətbiq etsək bizə öyrənmək daha rahat olar.
T-testi nədir?
Reqresiya testlərinin içində nisbətən daha asan test hesab olunur. T-test edərkən biz sərbəst dəyişənin asılı dəyişən üzərində mühim təsiri olub olmadığı sualına cavab tapa bilərik. T-testi edə bilmək üçün bizə data, statistik proqram(mən eviewsdan istifadə edəcəm), sıfır hipotezası və t, ya da p dəyəri lazımdır.
Sıfır Hipotezası belə qurulmuşdur:
H₀: β₁=0
Yadınızdadırsa, β₁ X₁ dəyişəninin(sərbəst) Y(asılı) dəyişən üzərində təsirini müəyyən edirdi. Əgər verilən hipotezada o, 0a bərabər olduğu deyilirsə, deməli sərbəst dəyişənin asılı dəyişən üzərində mühüm(significant) təsiri yoxdur. Hipoteza adından da gördündüyü kimi bir mülahizədir, onu qəbul və ya təkzib etmək mümkündür. Testin də əsas məqsədi budur: Biz hipotezanın düzgün olub olmamağını yoxlayırıq. Ola bilər ki sərbəst dəyişənin asılı dəyişən üzərində mühüm təsiri yoxdur, və ya vardır.
Testi edərkən özümüzə verəcəyimiz sual artıq aydındır: Sıfır Hipotezası doğrudur ya yox, başqa sözlə mühüm təsir var ya yox.
İndi gələk testin riyazi hissəsinə. Bunun üçün bizə t dəyəri lazımdır. T dəyərini tapmaq üçün biz β₁i standart xəta payına bölməliyik. Bu ədədləri almaq üçün isə ən effektiv yol statistik proqramlardan istifadə etməkdir. Keçən yazıda üstündə işlədiyimiz Eviews nəticəsini yenidən nəzərdən keçirək:
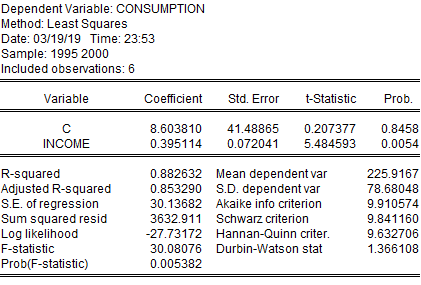
Göründüyü kimi, T dəyəri β₁in standart xətaya olan nisbətindən alınıb(0.395114/0.072041). Gələk tetsin kuliminasiya nöqtəsinə: əminlik intervalları(confidence level).
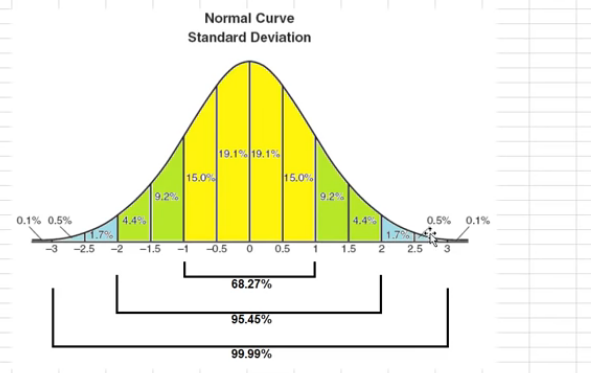
Məsələn götürək 95% əminlik intervalı. Bu zaman bizim kritik dəyərimiz(critical value) 1.96 olacaq. Bu isə o deməkdir ki, əgər biz t dəyərini -1.95 ilə +1.95 arasında bir rəqəm alsaq, biz əminlik intervalının içinə düşürük və deyirik ki 95% əminik ki, biz Sıfır hipotezini rədd edə bilmərik. Çünki biz əminlik intervalının daxilinə düşdük. Qeyd edim ki, rədd edə bilməmək, qəbul etmək demək deyil. Sadəcə olaraq biz bu fikri rədd də edə bilmərik. Məsələn biz t dəyərini 1.23 alsaq, biz -1.96 və 1.96 arasında biryerdəyik, deməli əminlik intervalına düşürük və hipotezanı rədd edə bilmərik. Yox əgər deyək ki, biz 2.74 aldıq. Bu rəqəm 1.96dan böyükdür. Deməli biz əminlik intervalından kənara düşürük, deməli hipotezanı rədd edə bilərik. (Eyni proses -1.96dan kiçik rəqəmlər üçün də doğrudur. Çünki biz yenə də əminlik intervalından kənara düşəcəyik). İndi yada salaq ki, hipoteza nə deyirdi: Hipoteza deyirdi ki, sərbəst dəyişənin asılı dəyişən üzərində mühüm təsiri(significant impact) yoxdur. Əgər biz bu fikri rədd ediriksə, deyə bilərik ki dəyişənlər arasında mühüm təsir mövcuddur.
Yuxarıda verilən funksiyaya yenidən nəzər salaq: bizim t dəyərimiz 5.48dir. Bu isə 1.96dan böyükdür. Deməli biz 95%lik əminlik intervalından kənardayıq və hipotezanı rədd edə bilərik. Bu zaman biz deyirik ki, qazanılan pulun xərclənən pul üzərindəki mühüm təsiri vardır.
Bəs p dəyəri nə üçündür?
T dəyərini biz t test üçün istifadə edə bilərik. Amma p dəyəri ilə biz istənilən testdən dolğun nəticə çıxara bilərik. Öz misalımızı nəzərdən keçirək. P dəyərimiz 0.0054, başqa sözlə 0.54% verilib. Yəni bizim o intervala düşmək ehtimalımız verilmiş əminlik intervallarına düşmür. Biraz dərindən fikirləşin, tutaq ki, bizim əminlik intervalımız 99%dir. Yəni 1% qırağa düşmək ehtimalı var və bizim aldığımız rəqəm bu 1%dən aşağıdır. Deməli biz bu intervala düşmürük. Bu o deməkdir ki, biz bu hipotezanı rədd edə bilərik və deyirik ki, dəyişənlər arasında mühüm əlaqə vardır. Eyni prosesi 95% üçün də edə bilərik və yenə də bizim p dəyərimizin 5%dən aşağı olduğunu görürük və eyni nəticəni alırıq.
Gördündüyü kimi istər p, istərsə də f dəyəri ilə biz testi apara bilərik və aldığımız cavab da eyni olacaqdır. Ümumiləşdirmə üçün bir daha qeyd edim ki, əgər p dəyərimiz 1%(99% əminlik ehtimalında), 5%(95%əminlik intervalında) və digər faizlərdən aşağıdırsa, biz sıfır hipotezasını rədd edirik, böyük olduqda isə rədd edə bilmirik.
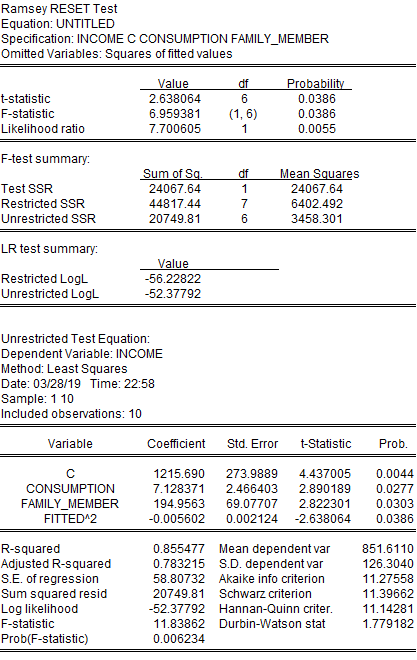
Sizə sadəcə p dəyərinin geniş miqyasda və daha ali testlərdə necə tətbiqi olunduğu haqqında qısa bir misal göstərəcəm. Ekonometrik modellər üzərində tətbiq edilən testlərdən biri də Ramsey Reset testdir. Ramsey Reset modeldə hər hansısa bir uyğunsuzluğu tapmaq üçün edilən bir testdir. Bu uyğunsuzluqlara nələr daxil ola bilər? Məsələn düşünün ki, siz su içmək istəyirsiz. Bu zaman sizin asılı dəyişəniniz sudan aldığınız xeyirdir. Gəlin sərbəst dəyişəni də su içdiyiniz stəkan sayı götürək. Birinci, ikinci, bəzən də üçüncü stəkan sizə xeyir verir çünki sizin susuzluğunuzu yatırır. Amma bir nöqtədən sonra (bu nöqtəyə threshold point deyilir) artıq içdiyiniz stəkan sizə və sağlamlığınıza ziyan vurur. Deməli bu dəyişənlər arasında ikili əlaqə var: bir nöqtəyə kimi müsbət, bu nöqtədən sonra isə mənfi əlaqə vardır. Buna, ekonometrikada kvadratik funksiya deyilir. Əgər biz bu dəyişəni modelə adi funksiya kimi daxil etsək, modeldə uyğunsuzluq olacaqdır. Tutaq ki stəkanı müsbət götürdüz. Bu o deməkdir ki, siz nə qədər çox su içsəz, bir o qədər yaxşı olar. Amma həqiqətdə 10 stəkan su içsəz həyatınızı riskə atarsınız. Ramsey Reset test modeldə bu kimi qanunauyğunsuzluqları tapmaq üçündür. Sıfır hipotezasında deyilir ki, modeldə problem yoxdur. Əgər biz testin sonunda bu fikri rədd etsək, deməli modeldə problem(misspecification) vardır.
Gəlin bir nümunəyə baxaq: (testin nəticəsi növbəti səhifədə qeyd edilmişdir)
Burda biz p dəyərini görə bilirik. Testin nəticəsinə görə, p dəyərimiz 0.0386, yəni 3.86% olmuşdur. Bu, 5%dən kiçikdir. Biz bu zaman deyə bilərik ki, 95% əminliklə biz sıfır hipotezasını rədd edirik və deyirik ki, modeldə problem vardır. Amma 99% əminlik intervalında biz hipotezanı rədd edə bilmirik və deyirik ki, bu əminlik intervalında biz modelin düzgün olduğunu fikirləşirik. Çünki bu faiz 1%dən böyükdür.
Ramsey Reset test sizə müəyyən qədər qaranlıq qala bilər, amma burda əsas məqsədim sizə p dəyərinin müxtəlif testlərdə necə tətbiq edilməsini göstərmək idi. T-testi əgər başa düşsəz, siz bir-iki nümunə ilə artıq daha çətin testlərə keçə bilərsiniz. Məsələn məsləhətim odur ki, növbəti dayanacağınız F-Test olsun. F-testi eviewsda Wald test vasitəsilə eləmək olar. F-testdə birdən artıq sərbəst dəyişənin asılı dəyişən üzərində ortaq təsirini(joint impact) müəyyən edə bilər. Siz orda F dəyərini və p dəyərini görəcəksiz. Sizə tövsiyəm bütün testləri p dəyəri ilə, izah etdiyim məntiqlə həll edəsiniz. Çünki bu necə deyərlər beynəlxalq standartdır və testlərin demək olar ki hamısında keçərlidir.
Daha çox oxu:

