Reqressiya Analizi nədir?

Yəqin ki, data analitikası ilə elementar da olsa tanışlığı olan hər kəs data analitikasının əsasının reqressiya analizi olduğunun fərqindədir. Bu sahə üzrə təhsili olan insanların reqressiya funksiyasının ilkin mahiyyətinin dərk edilməsində heç bir çətinlik çəkmədikləri sübuta əsası olmayan faktdır.

Sizə data analizi ilə yalnız ali məktəbdə keçirilən ekonometrika və statistika fənləri ilə və Data SoCool-da dərs almış sıradan bir tələbə kimi deyə bilərəm ki, reqressiya analizi mənim akademik və iş həyatımda qarşılaşdığım öyrənilməsi və dərk edilməsi nisbətən daha asan olan mövzulardan biri, bəlkə də birincisidir.

Amma bunun bəhs edildiyi kimi, y=kx + b düsturu qədər asan olmadığı da bir sirr deyil. Mənim məqaləmi oxuyanların bir çoxunun da “Reqressiyanın nəyi asandır?” deyə düşünməsinin də təməl səbəbi reqressiya analizini ilk öyrənməyə başlayarkən onun kx+b qədər asan olmasını düşünmələridir.

Bəs görəsən problem nədədir və yaxud da doğrudanmı reqressiya bu qədər asan mövzudur?

Reqressiya analizinin tətbiqi

Reqressiya analizi bir və yaxud bir neçə müstəqil dəyişənin asılı dəyişənə necə təsir göstərməsini müəyyən edən və bu əlaqə üzərində bir sıra testlərin tətbiq edilməsinə imkan yaradan bir funksiyadır. Ümumi düsturu isə belədir:

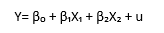
Bu düstura istədiyiniz qədər x, yəni sərbəst dəyişən əlavə etmək mümkündür, yetər ki, onun y-i, yəni asılı dəyişən üzərində məntiqi və ya statistik təsiri olsun. Məsələyə adı çəkilən birinci dəyişənlərin və əmsalların (betaların) izahı ilə başlayaq.

Sadə bir misal götürək: hər hansı bir şəxsin qazandığı pulla xərclədiyi pul arasında əlaqə. Aydın məsələdir ki, qeyd olunan şərtlər çərçivəsində bizim asılı dəyişənimiz xərclədiyimiz pul, sərbəst dəyişənimiz isə qazandığımız puldur. Əlbəttə, qazandığımız pul da bir sıra faktorlardan asılıdır, amma bu, başqa bir reqressiya funksiyasının mövzusudur, istənilən halda araşdırıla bilər. Bəzən sərbəst dəyişənlərin belə öz aralarında müxtəlif cür əlaqələri olur, bu da eyni formada araşdırıla bilər. Növbəti hissələrdə bu haqda da danışmağa çalışacağam.

Deməli, qazandığımız pul (x) xərclədiyimiz pula (y) təsir göstərir. Sual yaranır ki, necə?

Bu sualın cavabını isə bizə əmsallar izah edir. β₁ x dəyişdikdə y-in necə azalıb-artmasını izah edir. Məsələn, β₁ əgər 10-a bərabərdirsə, x-in 1 vahid artması y-i 10 ədəd (və yaxud da kəmiyyət nə ilə ifadə olunursa), β₀ isə sərbəst dəyişən 0-a bərabər olduqda və digər bütün faktorlar constant (ceteris-paribus) götürüldükdə, yəni u=0 olduqda y-in nəyə bərabər olduğunu göstərir. Sual yaranır ki, bəs bu əmsallar necə hesablanır? Əmsalların hesablanmasının riyazi üsulu var və onu deyim ki, xüsusən də böyük data olduqda hesablanması olduqca çətin və xəta ehtimalı çoxdur. Müasir texnologiya vasitəsilə isə bunu tapmaq çox rahatdır. Məsələn, mən öz hesablamalarımda Eviews statistik proqramından istifadə edirəm. R, Stata və s. kimi proqramlardan da istifadə etmək mümkündür. Sadəcə olaraq bu proqramlara girib datanı daxil edirsiniz və LS(Ən kiçik kvadratlar üsulu) ilə proqram sizə avtomatik olaraq əmsalları çıxardır. Köməklik üçün Eviews-a daxil edilən funksiyanı yaza bilərəm: “LS consumption(sizin asılı dəyişəniniz, datada olduğu kimi yazılmalıdır) c income(sərbəst dəyişən) fam_mem(family members, ikinci sərbəst dəyişən)”

Növbəti sual isə yəqin ki, reqressiya funksiyasının son həddi ilə bağlıdır. Əsasən u,v ilə ifadə olunur. Bu, residual və ya error term adlanır və funksiyanın xəta payı sayılır. Onu da deyim ki, reqressiya analizinin beynimdə qalmış bütün qaranlıq hissələrini residualı öyrənərkən başa düşmüşdüm. Bunu isə actual value (həqiqi dəyər) və estimated value (təxmin edilən dəyər) ilə başa düşmək mümkündür. Düşünün ki, Azərbaycanın bütün əhalisindən qazandıqları və xərclədikləri pulun nə qədər olması barədə sorğu keçiririk və əldə edilən datanı proqram vasitəsilə analiz edib verilən nəticəni alırıq:

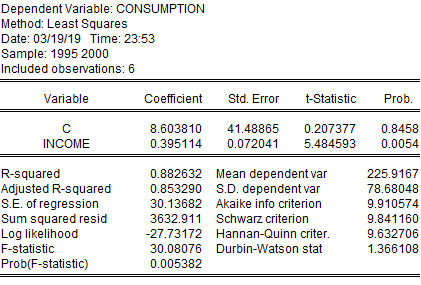
Consumption =8.60 + 0.39 * income + u[1]

Aydındır ki, aylıq gəlir 0 manat olsa belə, fərd yaşamaq üçün 8 manat 60 qəpik xərcləməlidir. Məsələn, bu, yaşayış minimumunu müəyyənləşdirmək üçün ideal bir metod ola bilər(təbii ki, bizim rəqəm reallığı əks etdirmir). İkinci bir nəticəyə gəlmək olar ki, gəlir 1 manat artdıqda, xərclənən pul 39 qəpik artır.[2] Əmsalların ümumi mənası da qeyd etdiyim kimi sərbəst dəyişənlə asılı dəyişənin arasında təsiri müəyyən edir. Təkrar üçün bir daha qeyd edim ki, 0.39 manat gəlirin 1 manat artdığı təqdirdə xərclənən pulun nə qədər dəyişdiyini müəyyən edir.

Bunu öz proqnozlarımızda da istifadə edə bilərik. Məsələn, ayda ortalama 500 manat gəliri olan şəxsin nə qədər xərclədiyini təxmin edə bilərik. Bunun üçün sadəcə olaraq, income yerinə 500 yazıb xərclənən pulu tapırıq: 203.06 manat(8.06+0.39*500). Amma real dataya baxdıqda görürük ki, 500 manat gəliri olan şəxs əslində 203 yox, 300 manat xərcləyir. Aradakı fərqə biz error term, və ya xəta payı deyirik. Verilən bu nümunədən sonra, fikrimcə, xəta payı daha anlaşılan oldu. Gələcək üçün biz proqnoz edəndə xəta payının rolunu nəzərə almalıyıq.

Bəs verilən xəta payını biz necə minimallaşdıra bilərik?

Bunun üçün bizə R²-dan istifadə etmək lazım olur. Daha dərin testlərlə sonrakı məqalələrdə tanış olacağıq, amma Eviews-un bizə verdiyi nəticədə rahatlıqla R² dəyərini görə bilərik və bu dəyər asılı dəyişəndə baş verən dəyişikliyin neçə faizinin sərbəst dəyişənlərdən asılı olduğunu bildirir. Kiçik bir izah verim: əgər bizim gəlir-xərc funksiyasında R² 0.88(88%) verilibsə, deməli xərclənən pulda baş verən 1 manat artımın 88%i gəlirdə baş verən artımla izah oluna bilər. Digər 12% isə modeldə olmalı olan digər dəyişənlərdən, məsələn, ailə üzvlərinin sayından asılıdır. Nəzərinizə çatdırım ki, R² 1-ə nə qədər yaxın olsa, bir o qədər yaxşıdır, lakin 1-ə bərabər olması demək olar ki, mümkün deyil. Əgər bu rəqəm 1-ə bərabərdirsə, reqressiya analizini davam etdirməyin heç bir mənası yoxdur, çünki modeldə artıq analizə ehtiyac yoxdur, hər şey aydın verilib.

Ümumən praktiki nümunələrdə düşünməyə başlasanız, görəcəksiniz ki, bu dəyərin 1-ə bərabər olması, demək olar ki, heç bir halda mümkün deyil. Sonda bir faktı da qeyd edim ki, R² özü belə tam düzgün məlumat vermir. Məsələn, biz modelə tamamilə aidiyyatı olmayan hansısa dəyişəni əlavə etsək, R² artar. Tutaq ki, modelə Barcelona futbol klubunun transfer xərclərini əlavə edirik, bunun bizim modelə heç bir halda aidiyyatı yoxdur və məntiqi əlaqədən söhbət getmir. Amma modelə daxil etdikdə, R² dəyərinin artdığını müşahidə edirik və bu bizə yanlış informasiya verir, çünki bu dəyər istənilən halda sərbəst dəyişənlərin sayı artdıqda artır. Artırılan dəyişənin mühüm olub olmadığını isə başqa indikatorlar və testlərlə müəyyən etmək olur ki, bu da növbəti yazıların mövzusudur.